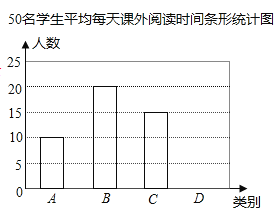
题目内容
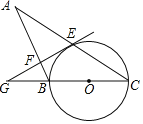
【题目】把△ABC放置在平面直角坐标系中,点A的坐标为(0,8),点B的坐标为(-6,0),点C的坐标为(8,0),M,N分别是线段AB,AC上的点,将△AMN沿直线MN翻折后,点A落在x轴上的A′处.
![]() Ⅰ
Ⅰ![]() 当MN∥x轴时,判断△A'CN的形状.
当MN∥x轴时,判断△A'CN的形状.
![]() Ⅱ
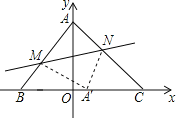
Ⅱ![]() 如图,当A'M⊥AB时.
如图,当A'M⊥AB时.
①求A'的坐标;②求MN的长.
![]() Ⅲ
Ⅲ![]() 当△A'MB是等腰三角形时,直接写出A'的坐标.
当△A'MB是等腰三角形时,直接写出A'的坐标.
【答案】(Ⅰ)等腰直角三角形;(Ⅱ)①![]() ,
,![]() ;②
;②![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]()
【解析】
(Ⅰ)得出∠ANM=∠A'NM=∠ACO=45°,则∠A'NC=90°,即可证出△A'NC为等腰直角三角形;
(Ⅱ)①设MA'=x,则BM=10-x,得出![]() ,解得x=
,解得x=![]() ,求出A'B,即可得出答案;
,求出A'B,即可得出答案;
②证明△AMN∽△ACB,可得出答案;
(Ⅲ)分三种情况,①当MB=MA'时,②当MA'=A'B时,③当BM=BA'时,可求出OA'的长,则答案可求出.
解:(Ⅰ)∵点A的坐标为(0,8),点B的坐标为(-6,0),点C的坐标为(8,0),
∴OA=OC=8,OB=6,
∵∠AOC=90°,
∴∠ACO=45°,AB=![]() ,AC=
,AC=![]() OA=
OA=![]() ,
,
![]() 将
将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 落在
落在![]() 轴上的
轴上的![]() 处,
处,
![]() ,
,![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() △
△![]() 为等腰直角三角形,
为等腰直角三角形,
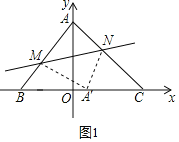
(Ⅱ)①当![]() 时,
时,![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
![]() ,
,
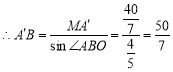 ,
,
![]() ,
,
![]() 的坐标为
的坐标为![]() ,
,![]() ;
;
②![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
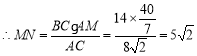 ;
;
(Ⅲ)①当![]() 时,
时,![]() 与点
与点![]() 重合,则
重合,则![]() ,
,
②当![]() 时,设
时,设![]() ,
,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
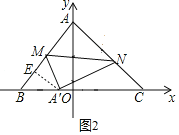
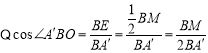 ,
,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
③当![]() 时,过点
时,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
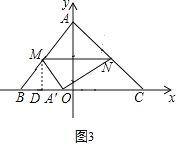
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
解得:![]() (负值舍去),
(负值舍去),
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
综合以上可得,当△![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标为
的坐标为![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.

练习册系列答案
相关题目