题目内容
【题目】如图,矩形OABC的边OA在x轴上,OA=10cm,OC在y轴上,且OC=4cm,P为OA 的中点,动点Q从C点出发,沿着CB以每秒1cm的速度运动(Q到B点时停止运动),当△OPQ是以OP为腰的等腰三角形时,点Q的运动时间=_______.
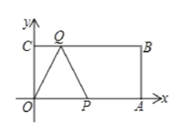
【答案】2秒或3秒或8秒
【解析】
分OQ=OP和OP=QP两种情况分别讨论,再结合勾股定理求解即可.
解:∵四边形OABC为矩形,
∴∠OCQ=90°,
∵OA=10,OC=4,P为OA的中点,
∴OP=5,
当OQ=OP=5时,
CQ=![]() ,
,
∴t=3;
当OP=QP时,如图,作PH⊥BC于H,
若点Q在点H左侧,
∵∠POC=∠OCH=∠CHP=90°,
∴四边形POCH为矩形,
∴PH=OC=4,CH=OP=5,
∴QH=![]() ,
,
∴CQ=CH-QH=5-3=2,即t=2;
若点Q在点H右侧,同理可得,CQ=5+3=8,即t=8.
故答案为:2秒或3秒或8秒.


练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目