题目内容
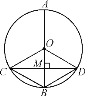
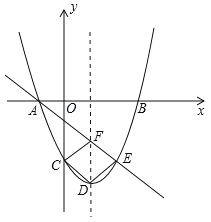
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在该圆内.将正方形ABCD绕点A逆时针旋转,当点D第一次落在圆上时,点C旋转到C′,则∠C′AB=__°.
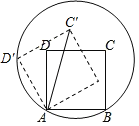
【答案】75
【解析】
如图,分别连接OA、OB、OD′、OC、OC′,证明△OAB和△OAD′都为等边三角形,则∠OAB=∠OAD′=60°,所以∠D′AB=120°;再证明∠D′AC′=45°,然后计算∠D′AB﹣∠D′AC′即可.
解:如图,分别连接OA、OB、OD′、OC、OC′;
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°;
同理可得△OAD′为等边三角形,
∴∠OAD′=60°,
∴∠D′AB=60°+60°=120°;
∵AC′为正方形AB′C′D′的对角线,
∴∠D′AC′=45°,
∴∠C′AB=∠D′AB﹣∠D′AC′=120°﹣45°=75°.
故答案为:75.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目