题目内容
【题目】已知抛物线![]() 经过点
经过点![]() ,点
,点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的顶点
的顶点![]() ,且
,且![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,若把抛物线上下平移,使抛物线的顶点在直线
,若把抛物线上下平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ),再把抛物线左右平移,使抛物线的顶点在直线
),再把抛物线左右平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ).
).
(1)求抛物线![]() 的解析式.
的解析式.
(2)判断以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设点![]() 、
、![]() 在直线
在直线![]() 上(点
上(点![]() 在点
在点![]() 的下方),当
的下方),当![]() 与
与![]() 相似时,求
相似时,求![]() 、
、![]() 的坐标(直接写出结果).
的坐标(直接写出结果).

【答案】(1)![]() ;(2)相离,理由详见解析;(3)
;(2)相离,理由详见解析;(3)![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]()
【解析】
(1)将点A、B的坐标代入![]() 即可求出解析式;
即可求出解析式;
(2)求出点N、C的坐标,计算NC的长度即可求解;
(3)分点F在直线![]() 下方,上方两种情况求解.
下方,上方两种情况求解.
(1)将点A、B的坐标代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)∵![]() ,
,
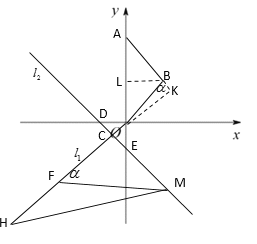
∴顶点坐标是(2,2),
将点P的坐标代入直线![]() 中,得2k=2,即k=1,
中,得2k=2,即k=1,
∴直线![]() 的解析式是y=x,
的解析式是y=x,
设点M(2,m),代入直线![]() 的解析式中,得m=-4,
的解析式中,得m=-4,
∴点M的坐标是(2,-4),
设点N的坐标是(n,-4),代入![]() 的解析式中,得n=-4,
的解析式中,得n=-4,
∴点N的坐标是(-4,-4),
同理:D(-2,0),E(0,-2),
联立![]() 、
、![]() 得
得![]() ,得
,得![]() ,
,
∴C(-1,-1),
∴OC=![]() ,
,
∴![]() ,
,
∵点C在直线y=x上,
∴∠COE=∠OEC=45°,
∴∠OCE=90°,即NC⊥![]() ,
,
∵NC=![]()
∴以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 相离;
相离;
(3)①当点F在直线![]() 下方时,
下方时,
设![]() ,
,
∵点A、B的坐标分别为(0,6),(1,3),
∴AO=6,AB=BO=![]() ,
,
过点B作BL⊥y轴于L,则![]() ,
,![]() ,
,
∴OK=![]() ,
,
∴![]() ,
,
∵等腰△MHF和等腰△OAB相似,
∴∠HFM=∠ABO,则∠KBO=∠OFM=![]() ,
,
∵C(-1,-1),M(2,-4),
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴F(-5,-5),
∵FH=FM=![]() ,OH=OF+FH=
,OH=OF+FH=![]() ,
,
∴H(-10,-10);
②当点F在直线![]() 上方时,
上方时,
同理可得点F的坐标为(8,8),点H的坐标为(3,3)或(-10,-10);
综上,![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]()

 特高级教师点拨系列答案
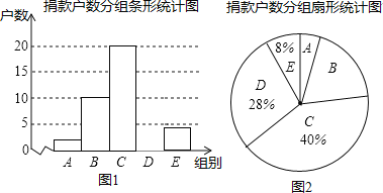
特高级教师点拨系列答案【题目】某社区组织“献爱心”捐款活动,并对部分捐款户数进行调查和分组统计,数据整理成如下统计图表(图中信息不完整).
捐款户数分组统计表
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<100 | 2 |
B | 100≤x<200 | 10 |
C | 200≤x<300 | c |
D | 300≤x<400 | d |
E | x≥400 | e |
请结合以上信息解答下列问题:
(1)本次调查的样本容量是______;
(2)d=______,并补全图1;
(3)图2中,“B”所对应扇形的圆心角为______度;
(4)若该社区有500户住户,根据以上信息估计全社区捐款不少于300元的户数是______.