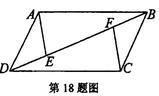
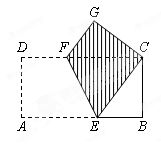
题目内容
如图，四边形ABCD中，∠A=90°，AD∥BC，BE⊥CD
于E交AD的延长线于F，DC=2AD，AB=BE．
小题1:求证：AD=DE
小题2:判断四边形BCFD的形状并说明理由．
于E交AD的延长线于F，DC=2AD，AB=BE．
小题1:求证：AD=DE
小题2:判断四边形BCFD的形状并说明理由．
略
考点：
（1）证明：∵
∴
∵
∴
∴
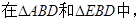
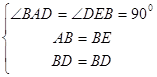
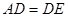
(2)解：∵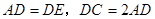
∴
∵
∴
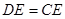
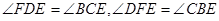
又∵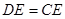
∴
∴
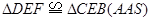
又∵
∴四边形BCFD是平行四边形.
∵，
∴
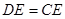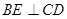
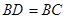
∴四边形BCFD是菱形.
点评：本题在菱形的判定上，根据垂直平分线的性质证明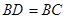容易被忽略。
（1）证明：∵
∴
∵
∴
∴
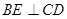
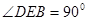
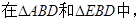
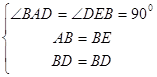
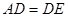
(2)解：∵
∴
∵
∴
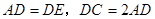
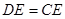
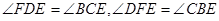
又∵
∴
∴
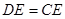
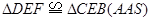
又∵
∴四边形BCFD是平行四边形.
∵
，∴
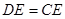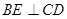
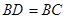
∴四边形BCFD是菱形.
点评：本题在菱形的判定上，根据垂直平分线的性质证明
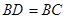容易被忽略。
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
中，
∥
，
的面积等于9，
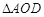的面积等于6，
，求
的长.
中，
，对角线
平分
，则梯形
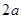，沿图中线段DE、CF将△ABC剪开，分成的三块图形恰能拼成正方形CFHG，如图1所示．请你解决如下问题：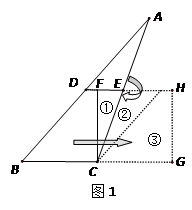
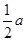．请你设计两种不同的分割方法，将△A′B′C′沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．
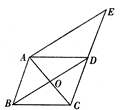
为平行四边形，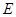
、
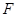为对角线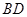
上的两点，且
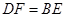，连接
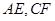。求证：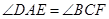
。
