题目内容
【题目】已知二次函数y＝﹣x2+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（ ）
A.﹣1≤t≤0B.﹣1≤t
C.
D.t≤﹣1或t≥0
【答案】A
【解析】
找到最大值和最小值差刚好等于5的时刻，则t的范围可知．
解：如图1所示，当t等于0时，
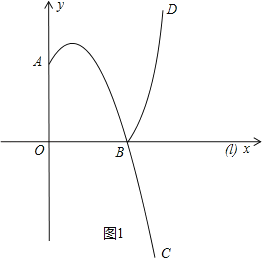
∵y＝﹣（x﹣1）2+4，
∴顶点坐标为（1，4），
当x＝0时，y＝3，
∴A（0，3），
当x＝4时，y＝﹣5，
∴C（4，﹣5），
∴当t＝0时，
D（4，5），
∴此时最大值为5，最小值为0；
如图2所示，当t＝﹣1时，
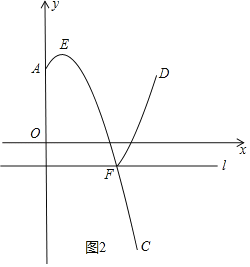
此时最小值为﹣1，最大值为4．
综上所述：﹣1≤t≤0，
故选：A．
练习册系列答案
相关题目
