题目内容
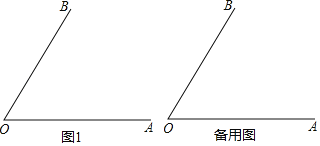
【题目】已知∠AOB=60°,P为它的内部一点,M为射线OA上一点,连接PM,以P为中心,将线段PM顺时针旋转120°,得到线段PN,并且点N恰好落在射线OB上.
(1)依题意补全图1;
(2)证明:点P一定落在∠AOB的平分线上;
(3)连接OP,如果OP=2![]() ,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
【答案】(1)详见解析;(2)详见解析;(3)OM+ON=6,值不变.
【解析】
(1)根据要求画出图形即可;
(2)作PE⊥OA于E,PF⊥OB于F.证明△PEM≌△PFN(AAS),推出PE=PF,理由角平分线的判定定理即可解决问题;
(3)理由全等三角形的性质证明OE=OF,FN=EM,求出OE,OF即可解决问题.
解:(1)图形如图所示:
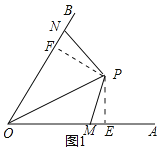
(2)作PE⊥OA于E,PF⊥OB于F.
∵∠PEO=∠PFO=90°,∠EOF=60°,
∴∠EPF=∠MPN=120°,
∴∠EPM=∠FPN,
∵PM=PN,∠PEM=∠PFN=90°,
∴△PEM≌△PFN(AAS),
∴PE=PF,
∵PE⊥OA于E,PF⊥OB于F,
∴OP平分∠AB,
∴点P在∠AOB的角平分线上.
(3)结论:OM+ON=6,值不变.
理由:∵∠PEO=∠PFO=90°,OP=OP,PE=PF,
∴Rt△OPE≌Rt△OPF(HL),
∴OE=OF,
∵OP=![]() ,∠POE=∠POF=30°,
,∠POE=∠POF=30°,
∴OE=OF=OPcos30°=3,
∵△PEM≌△PFN,
∴ME=FN,
∴OM+ON=OE﹣EM+OF+FN=2OE=6.

练习册系列答案
相关题目