题目内容
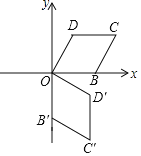
【题目】如图,在菱形OBCD中,OB=1,相邻两内角之比为1:2,将菱形OBCD绕顶点O顺时针旋转90°,得到菱形OB′C′D′视为一次旋转,则菱形旋转45次后点C的坐标为_____.
【答案】(![]() ,﹣
,﹣![]() )
)
【解析】
先求出菱形的内角度数,过![]() 作
作![]() 轴于
轴于![]() 点,在
点,在![]() △
△![]() 中,利用特殊角度数及边长求解
中,利用特殊角度数及边长求解![]() 和
和![]() 长,则
长,则![]() 点坐标可求,由
点坐标可求,由![]() ,得出菱形4次旋转一周,4次一个循环,由
,得出菱形4次旋转一周,4次一个循环,由![]() ,得出菱形旋转45次后点
,得出菱形旋转45次后点![]() 与点
与点![]() 重合,即可得出答案.
重合,即可得出答案.
解:∵四边形OBCD是菱形,相邻两内角之比为1:2,
∴∠C=∠BOD=60°,∠D=∠OBC=120°.
根据旋转性质可得∠OB′C′=120°,
∴∠C′B′H=60°.
过C′作C′H⊥y轴于点H,如图所示:
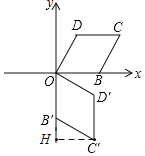
在Rt△C′B′H中,B′C′=1,
![]() ,
,![]() .
.
![]() .
.
![]() 坐标为
坐标为![]() ,
,![]() ,
,
∵360°÷90°=4,
∴菱形4次旋转一周,4次一个循环,
∵45÷4=11……1,
![]() 菱形旋转45次后点
菱形旋转45次后点![]() 与点
与点![]() 重合,坐标为
重合,坐标为![]() ,
,![]() ;
;
故答案为:![]() ,
,![]() .
.

练习册系列答案
相关题目