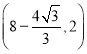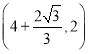题目内容
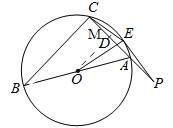
【题目】(2016广西柳州市)如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足![]() =PAPC,连接CE,AE,OE,OE交CA于点D.
=PAPC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP=![]() AC,求证:DO=DP.
AC,求证:DO=DP.

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)利用两边对应成比例,夹角相等,两三角形相似即可;
(2)连接BE,转化出∠OEB=∠PCE,又由相似得出∠PEA=∠PCE,从而用直径所对的圆周角是直角,转化出∠OEP=90°即可;
(3)构造全等三角形,先找出OD与PA的关系,再用等积式找出PE与PA的关系,从而判断出OM=PE,得出△ODM≌△PDE即可.
(1)∵![]() =PAPC,
=PAPC,
∴![]() ,
,
∵∠APE=∠EPC,
∴△PAE∽△PEC;
(2)如图1,连接BE,
∴∠OBE=∠OEB,
∵∠OBE=∠PCE,
∴∠OEB=∠PCE,
∵△PAE∽△PEC,
∴∠PEA=∠PCE,
∴∠PEA=∠OEB,
∵AB为直径,∴∠AEB=90°,
∴∠OEB+∠OEA=90°,
∵∠PEA+∠OEA=90°,
∴∠OEP=90°,
∵点E在⊙O上,
∴PE是⊙O的切线;

(3)如图2,过点O作OD⊥AC于M,
∴AM=![]() AC,
AC,
∵BC⊥AC,
∴OD∥BC,
∵∠ABC=30°,
∴∠AOD=30°,
∴OD=![]() AM=
AM=![]() AC,
AC,
∵AP=![]() AC,
AC,
∴OD=![]() AP,
AP,
∵PC=AC+AP=2AP+AP=3AP,
∴![]() =PA×PC=PA×3PA,
=PA×PC=PA×3PA,
∴PE=![]() PA,
PA,
∴OD=PE,
∵∠PED=∠OMD=90°,∠ODM=∠PDE,
∴△ODM≌△PDE,
∴OD=DP.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目