题目内容
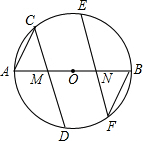
如图，△ABC中，∠A=60°，以BC为直径作⊙O分别交AB、AC于D、E，
（1）求证：AB=2AE；
（2）若AE=2，CE=1，求BC．
（1）求证：AB=2AE；
（2）若AE=2，CE=1，求BC．
（1）证明：连接BE，
∵BC是⊙O的直径，
∴∠BEC=90°，
即∠AEB=90°，
∵∠A=60°，
∴∠ABE=30°，∴AB=2AE；
（2）∵AE=2，
∴AB=2AE=4，
∴BE=
=2
，
∵CE=1，
∴BC=
=
．
∵BC是⊙O的直径，
∴∠BEC=90°，
即∠AEB=90°，
∵∠A=60°，
∴∠ABE=30°，∴AB=2AE；
（2）∵AE=2，
∴AB=2AE=4，
∴BE=
| AB2-AE2 |
| 3 |
∵CE=1，
∴BC=
| BE2+CE2 |
| 13 |
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
