题目内容
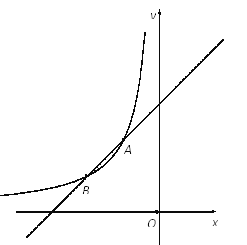
【题目】如图,函数![]() (x<0)与y=ax+b的图象交于点A(-1,n)和B(-2,1),直线y=mx与
(x<0)与y=ax+b的图象交于点A(-1,n)和B(-2,1),直线y=mx与![]() (x<0)的图象交于点P,与y=-x+1的图象交于点Q,定义∠PAQ为这个函数的“函数角”.
(x<0)的图象交于点P,与y=-x+1的图象交于点Q,定义∠PAQ为这个函数的“函数角”.
(1)求k,a,b的值;
(2)当m=-![]() 时,求这个函数的“函数角”的度数.
时,求这个函数的“函数角”的度数.
(3)若射线AP与x轴交于点N(a,0),当这个函数的“函数角”的度数不小于120°时,直接写出m的取值范围.
【答案】(1)k=-2;a=1,b=3;(2)函数角为90°;(3)-2<m≤2![]() -5或m≤-7-3
-5或m≤-7-3![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 代入函数
代入函数![]() (
(![]() )即可求得
)即可求得![]() 的值,函数
的值,函数![]() (
(![]() )的图象还经过点
)的图象还经过点![]() 即可求出
即可求出![]() 把点
把点![]() 的坐标代入函数
的坐标代入函数![]() 即可求得
即可求得![]() 的值.
的值.
![]() 根据函数角的定义求解即可.
根据函数角的定义求解即可.
![]() 直接写出取值范围即可.
直接写出取值范围即可.
试题解析:(1)∵ 函数![]() (
(![]() )的图象经过点
)的图象经过点![]()
∴![]() ,得
,得![]()
∵ 函数![]() (
(![]() )的图象还经过点
)的图象还经过点![]()
∴![]() ,点A的坐标为
,点A的坐标为![]()
∵ 函数![]() 的图象经过点A和点B,
的图象经过点A和点B,
得![]()
(2)当![]() 时,
时, ![]() 与
与![]() 的交点为
的交点为![]()
∴点P与点B重合.
∵![]() 与
与![]() 互相垂直,
互相垂直,
∴函数角为90°.
(3)如图直线![]() 经过点
经过点![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,
垂直,

分别求出当![]() 时,
时, ![]() 的值.
的值.
再通过观察图象可知:当![]() 或
或![]()
![]()

练习册系列答案
相关题目