题目内容
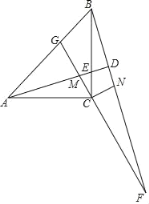
【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
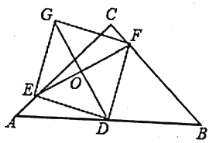
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
【答案】(1)详见解析;(2)当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4
【解析】
(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;
(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2![]() ,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
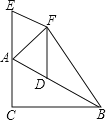
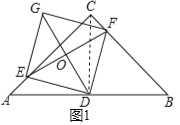
(1)证明:连接CD,如图1所示.
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
D是AB的中点,
∴![]()
在![]() 和
和![]() 中
中![]() ,
,
∴ ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵O为EF的中点,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形EDFG是正方形;
(2)解:过点D作![]() 于E′,如图2所示.
于E′,如图2所示.

∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() ,点E′为AC的中点,
,点E′为AC的中点,
∴![]() (点E与点E′重合时取等号).
(点E与点E′重合时取等号).
∴![]()
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目