题目内容
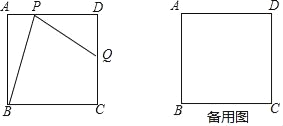
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() (0<x<2);(3)见解析
(0<x<2);(3)见解析
【解析】试题分析:(1)延长PQ交BC延长线于点E.设PD=x,由∠PBC=∠BPQ可得EB=EP,再根据AD//BC,QD=QC可得PD=CE,PQ=QE,从而得BE=EP= x+2, QP=![]() ,在Rt△PDQ中,根据勾股定理可得
,在Rt△PDQ中,根据勾股定理可得![]() ,从而求得
,从而求得![]() 的长,再根据正切的定义即可求得;
的长,再根据正切的定义即可求得;
(2)过点B作BH⊥PQ,垂足为点H,联结BQ,通过证明Rt△PAB Rt△PHB,得到AP = PH =x,通过证明Rt△BHQ Rt△BCQ,得到QH = QC= y,在Rt△PDQ中,根据 勾股定理可得PD2+QD2=PQ2,代入即可求得;
(3)存在,根据(2)中的两对全等三角形即可得.
试题解析:(1)延长PQ交BC延长线于点E,设PD=x,
∵∠PBC=∠BPQ,
∴EB=EP,
∵四边形ABCD是正方形,
∴AD//BC,∴PD∶CE= QD∶QC= PQ∶QE,
∵QD=QC,∴PD=CE,PQ=QE,
∴BE=EP= x+2,∴QP=![]() ,
,
在Rt△PDQ中,∵![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() ,∴
,∴![]() ;
;
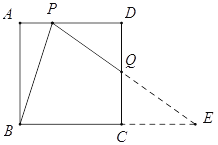
(2)过点B作BH⊥PQ,垂足为点H,联结BQ,
∵AD//BC,∴∠CBP=∠APB,∵∠PBC=∠BPQ,∴∠APB=∠HPB,
∵∠A=∠PHB=90°,∴BH = AB =2,∵PB = PB,∴Rt△PAB![]() Rt△PHB,
Rt△PHB,
∴AP = PH =x,
∵BC = BH=2,BQ = BQ,∠C=∠BHQ=90°,
∴Rt△BHQ![]() Rt△BCQ,∴QH = QC= y
Rt△BCQ,∴QH = QC= y
在Rt△PDQ中,∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;

(3)存在,∠PBQ=45°.
由(2)可得, ![]() ,
, ![]() ,
,
∴![]() .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?