题目内容
【题目】已知:如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,P是边AB上一动点,PE⊥CD,垂足为点E,PM⊥AB,交边CD于点M,AD=1,AB=5,CD=4.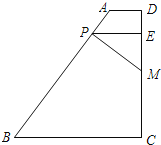
(1)求证:∠PME=∠B;
(2)设A、P两点的距离为x,EM=y,求y关于x的函数解析式,并写出它的定义域;
(3)连接PD,当△PDM是以PM为腰的等腰三角形时,求AP的长.
【答案】(1)详见解析;(2)0≤x≤![]() ;(3)当△PDM是以PM为腰的等腰三角形时,AP=
;(3)当△PDM是以PM为腰的等腰三角形时,AP=![]() 或AP=1.
或AP=1.
【解析】
(1)在四边形BCMP中,求出∠B+∠CMP=180°,又知∠PME+∠CMP=180°,于是证明出∠PME=∠B;
(2)作AH⊥BC于H,交PE于点F,首先证明出AF⊥PE,由于PF∥BH,列出比例等式,用x表示出PF和PE,再由△PEM∽△AHB列出y与x的关系式;
(3)分类讨论,当PM=PD和PM=DM分别根据等腰三角形的性质求出x的值,进而求出AP的值.
(1)证明:证法一:在四边形BCMP中,
∵∠B+∠C+∠CMP+∠MPB=360°,∠C=∠MPB=90°
∴∠B+∠CMP=180°.
而∠PME+∠CMP=180°,
∴∠PME=∠B.
证法二:∵DC⊥BC,PM⊥AB,且∠PME与∠B都为锐角,
∴∠PME=∠B.
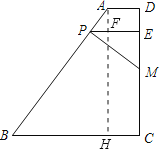
(2)作AH⊥BC于H,交PE于点F.
∵PE⊥CD,BC⊥CD,
∴PE∥BC.
∴AF⊥PE.
∵AH=CD=4,AB=5,
∴BH=3.
∵AD=1,
∴EF=1.
∵PF∥BH,
∴![]() ,
,
∴PF=![]() x,
x,
∴PE=![]() x+1.
x+1.
又∵∠PME=∠B,∠PEM=∠AHB=90°,
∴△PEM∽△AHB.
∴![]() ,
,
即![]()
∴y=![]()
∵PE=![]() x+1≤BC=4,
x+1≤BC=4,
∴x≤![]() ,
,
定义域为0≤x≤![]() .
.
(3)(ⅰ)当PM=PD时,DE=EM.![]() x=
x=![]() x+
x+![]() .
.
解得x=![]() ,即
,即![]() .
.
(ⅱ)当PM=DM时,
![]() (
(![]() x+1)=
x+1)=![]() x+
x+![]() x+
x+![]() .
.
解得x=1,即AP=1.
综上所述,当△PDM是以PM为腰的等腰三角形时,AP=![]() 或AP=1.
或AP=1.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.