题目内容
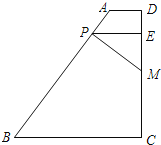
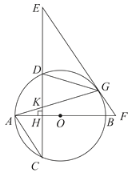
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
【答案】(1)见解析;(2)①见解析,②![]()
【解析】
(1)连接OG.根据切线的判定,证出∠KGE+∠OGA=90°,故EF是⊙O的切线.(2)①证∠E=∠AGD,又∠DKG=∠CKE,故△KGD∽△KGE.②连接OG.![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() ,在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即
,在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即![]() ;由勾股定理得:OH2+CH2=OC2,
;由勾股定理得:OH2+CH2=OC2,![]() ;在Rt△OGF中,
;在Rt△OGF中,![]() ,
,![]() ,
,![]()
(1)如图,连接OG.∵EG=EK,
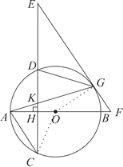
∴∠KGE=∠GKE=∠AKH,
又OA=OG,∴∠OGA=∠OAG,
∵CD⊥AB,∴∠AKH+∠OAG=90°,
∴∠KGE+∠OGA=90°,
∴EF是⊙O的切线.
(2)①∵AC∥EF,∴∠E=∠C,
又∠C=∠AGD,∴∠E=∠AGD,
又∠DKG=∠CKE,
∴△KGD∽△KGE.
②连接OG,如图所示.∵![]() ,AK=
,AK=![]() ,
,
设![]() ,∴
,∴![]() ,
,![]() ,则
,则![]()
KE=GE,AC∥EF,∴CK=AC=5k,∴HK=CK-CH=k.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设⊙O半径为R,在Rt△OCH中,OC=R,OH=R-3k,CH=4k,
由勾股定理得:OH2+CH2=OC2,![]() ,∴
,∴![]()
在Rt△OGF中,![]() ,∴
,∴![]() ,
,
∴![]()

 轻松暑假总复习系列答案
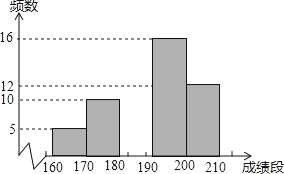
轻松暑假总复习系列答案【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
根据图表解决下列问题:
(1)本次共抽取了 名学生进行体育测试,表中,a= ,b= ,c= ;
(2)补全统计图;
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?