题目内容
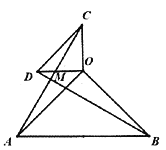
【题目】在![]() ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
ABCD中,E、F分别是AD、BC上的点,将平行四边形ABCD沿EF所在直线翻折,使点B与点D重合,且点A落在点A′处.
(1)求证:△A′ED≌△CFD;
(2)连结BE,若∠EBF=60°,EF=3,求四边形BFDE的面积.

【答案】(1)见解析;(2)![]() .
.
【解析】
由由翻折可知:AB=A′D,∠ABC=∠A′DF,∠EFB=∠EFD,由平行四边形的性质知,AB=CD,∠ABC=∠ADC,进一步可证∠FDC=∠A′DE, A′D=CD.再结合平行线的性质说明ED=DF,即可证明△A′ED≌△CFD;
(2)先证明四边形EBFD为菱形,从而BE=BF=3.过点E作EH⊥BC于点H,根据锐角三角函数的知识求出EH的长,然后利用三角形面积公式计算即可.
(1)证明:由翻折可知:
AB=A′D,∠ABC=∠A′DF,∠EFB=∠EFD,
∵四边形ABCD是平行四边形,
∴AB=CD,∠ABC=∠ADC,
∴∠ADC=∠A′DF,
∴∠FDC=∠A′DE,
∵AB=A′D,AB=CD,
∴A′D=CD.
∵AD∥BC,
∴∠DEF=∠EFB,
∵∠EFB=∠EFD,
∴∠DEF=∠EFD,
∴ED=DF,
∴△A′ED≌△CFD;
(2)解:∵AD∥BC,A′B∥DF,
∴四边形EBFD为平行四边形.
由(1)DE=DF,
∴四边形EBFD为菱形.
∵∠EBF=60°,
∴△BEF为菱形.
∵EF=3,
∴BE=BF=3.
过点E作EH⊥BC于点H,
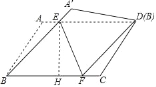
∴四边形BFDE的面积为:sin60°AEBF=![]() .
.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目