题目内容
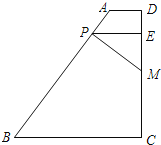
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m-2(m![]() 0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() <m≤1B.
<m≤1B. ![]() ≤m<1C. 1<m≤2D. 1<m<2
≤m<1C. 1<m≤2D. 1<m<2
【答案】A
【解析】
画出图象,利用图象可得m的取值范围
∵y=mx2-4mx+4m-2=m(x-2)2-2且m>0,
∴该抛物线开口向上,顶点坐标为(2,-2),对称轴是直线x=2.
由此可知点(2,0)、点(2,-1)、顶点(2,-2)符合题意.
①当该抛物线经过点(1,-1)和(3,-1)时(如答案图1),这两个点符合题意.
将(1,-1)代入y=mx2-4mx+4m-2得到-1=m-4m+4m-2.解得m=1.
此时抛物线解析式为y=x2-4x+2.
由y=0得x2-4x+2=0.解得x1=2-![]() ≈0.6,x2=2+
≈0.6,x2=2+![]() ≈3.4.
≈3.4.
∴x轴上的点(1,0)、(2,0)、(3,0)符合题意.
则当m=1时,恰好有(1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-1)、(2,-2)这7个整点符合题意.
∴m≤1.【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】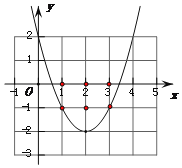
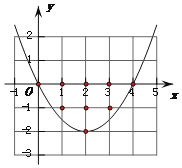
答案图1(m=1时)答案图2(m=![]() 时)
时)
②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意.
此时x轴上的点(1,0)、(2,0)、(3,0)也符合题意.
将(0,0)代入y=mx2-4mx+4m-2得到0=0-4m+0-2.解得m=![]() ,
,
此时抛物线解析式为y=![]() x2-2x.
x2-2x.
当x=1时,得y=![]() ×1-2×1=-
×1-2×1=-![]() <-1.∴点(1,-1)符合题意.
<-1.∴点(1,-1)符合题意.
当x=3时,得y=![]() ×9-2×3=-
×9-2×3=-![]() <-1.∴点(3,-1)符合题意.
<-1.∴点(3,-1)符合题意.
综上可知:当m=![]() 时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意,
时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意,
∴m=![]() 不符合题.
不符合题.
∴m>![]() .
.
综合①②可得:当![]() <m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
<m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
故选:A.

 名校课堂系列答案
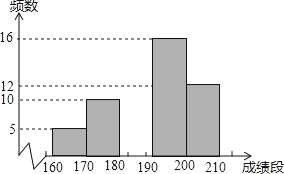
名校课堂系列答案【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校1000名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
根据图表解决下列问题:
(1)本次共抽取了 名学生进行体育测试,表中,a= ,b= ,c= ;
(2)补全统计图;
(3)“跳绳”数在180(包括180)以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?