题目内容
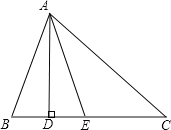
【题目】如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作FG⊥AC于点F，交AB的延长线于点G．
（1）求证：FG是⊙O的切线；
（2）若tanC=2，求
的值．
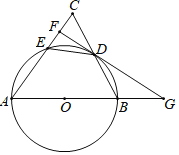
【答案】（1）证明见解析；（2）BG：GA=1：4．
【解析】（1）欲证明FG是⊙O的切线，只要证明OD⊥FG即可；
（2）由△GDB∽△GAD，设BG=a．可得
，推出DG=2a，AG=4a，由此即可解决问题.
（1）如图，连接AD、OD，
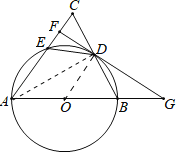
∵AB是直径，
∴∠ADB=90°，即AD⊥BC，
∵AC=AB，
∴CD=BD，
∵OA=OB，
∴OD∥AC，
∵DF⊥AC，
∴OD⊥DF，
∴FG是⊙O的切线；
（2）∵tanC=
=2，BD=CD，
∴BD：AD=1：2，
∵∠GDB+∠ODB=90°，∠ADO+∠ODB=90°，
∵OA=OD，
∴∠OAD=∠ODA，
∴∠GDB=∠GAD，
∵∠G=∠G，
∴△GDB∽△GAD，设BG=a．
∴，
∴DG=2a，AG=4a，
∴BG：GA=1：4．
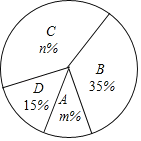
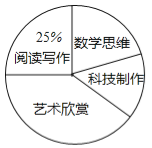
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
