Question

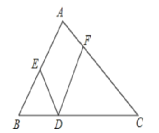
【题目】如图，△ACF≌△DBE，其中点A、B、C、D在一条直线上.

（1）若BE⊥AD，∠F=62°，求∠A的大小.

（2）若AD=9cm，BC=5cm，求AB的长.

Answer 1

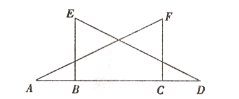
【答案】（1）∠A=28°；（2）AB =2 cm．

【解析】

（1）根据全等三角形的性质得到∠FCA=∠EBD=90°，根据直角三角形的性质计算即可；
（2）根据全等三角形的性质得到CA=BD，结合图形得到AB=CD，计算即可．

（1）∵BE⊥AD，

∴∠EBD=90°．

∵△ACF≌△DBE，

∴∠FCA=∠EBD=90°．

∴∠F+∠A=90°

∵∠F =62°，

∴∠A=28°．

（2）∵△ACF≌△DBE，

∴CA=BD．

∴CA-CB=BD-CB．

即AB=CD．

∵AD=9 cm, BC=5 cm，

∴AB+CD=9-5=4 cm．

∴AB=CD=2 cm．