题目内容
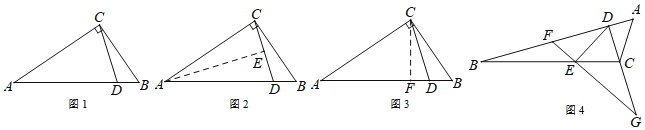
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.
∵AB⊥BC,∴∠B=90°.
∵AD∥BC,∴∠A=180°﹣∠B=90°,∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,
设AP的长为x,则BP长为8﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得:x=![]() ;
;
②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得:x=2或x=6,∴满足条件的点P的个数是3个.
故选C.

 阅读快车系列答案
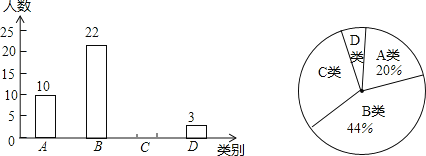
阅读快车系列答案【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩(s) | 频数(人数) |
A | 90<s≤100 | 4 |
B | 80<s≤90 | x |
C | 70<s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.