题目内容
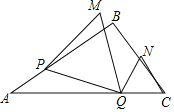
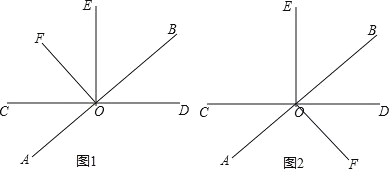
【题目】已知如图,直线![]() 相交于点
相交于点![]() .
.
(1)若∠AOC=35°,求![]() 的度数;
的度数;
(2)若∠BOD:∠BOC=2:4,求![]() 的度数;
的度数;
(3)在(2)的条件下,过点![]() 作
作![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)55°,(2)150°,(3)60°或120°
【解析】
(1)根据AOB共线即可知![]() +
+![]() +
+![]() =180°即可解得;
=180°即可解得;
(2)根据平角的定义可求出∠BOD,根据对顶角的定义可求出∠AOC,再根据角的和差关系可求∠AOE的度数;
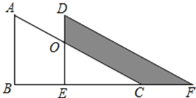
(3)先过点O作![]() ,再分两种情况根据角的和差关系来求∠EOF即可.
,再分两种情况根据角的和差关系来求∠EOF即可.
(1)∵∠AOC=35°,![]() ,
,
∴![]() =180°-
=180°-![]() -
-![]() =55°;-
=55°;-
(2)∵∠BOD:∠BOC=2:4,
∴![]() =180°×
=180°×![]() =60°,
=60°,
∴∠AOC=60°,
∴∠AOE=60°+90°=150°;
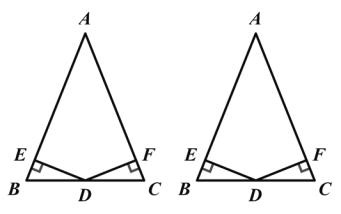
(3)如图1,∠EOF=150°-90°=60°,
或如图2,∠EOF=360°-150°-90°=120°,
故∠EOF的度数为60°或120°.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
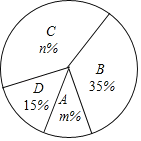
【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩(s) | 频数(人数) |
A | 90<s≤100 | 4 |
B | 80<s≤90 | x |
C | 70<s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.