Question

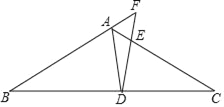
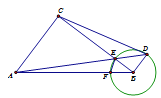
【题目】如图，已知在Rt△ABC中，∠ACB = 90o，AC =6，BC = 8，点F在线段AB上，以点B为圆心，BF为半径的圆交BC于点E，射线AE交圆B于点D（点D、E不重合）．

（1）如果设BF = x，EF = y，求y与x之间的函数关系式，并写出它的定义域；

（2）如果，求ED的长；

（3）联结CD、BD，请判断四边形ABDC是否为直角梯形？说明理由．

Answer 1

【答案】（1）（0＜x＜8）；（2）ED=；（3）四边形ABDC不可能为直角梯形．

【解析】试题分析：（1）在Rt△ABC中由勾股定理得到AB=10．过E作EH⊥AB，垂足是H，易得：EH= ，BH= ，FH= ．在Rt△EHF中，由勾股定理即可得到结论；

（2）取弧ED的中点P，联结BP交ED于点G．由 ，P是弧ED的中点，得到弧EP=弧EF=弧PD，进而得到∠FBE =∠EBP =∠PBD．由垂径定理得BG⊥ED，ED =2EG =2DG．易证△BEH≌△BEG，得到EH=EG=GD= ．解Rt△CEA得到CE，BE的长，从而得到结论．

（3）四边形ABDC不可能为直角梯形．分两种情况讨论：①当CD∥AB时，如果四边形ABDC是直角梯形，只可能∠ABD =∠CDB = 90o．由，即可得到结论．

②当AC∥BD时，如果四边形ABDC是直角梯形，只可能∠ACD =∠CDB = 90o．由∠ABD＞ 90o．即可得到结论．

试题解析：解：（1）在Rt△ABC中，AC=6，BC=8，∠ACB=90°，∴AB=10．

过E作EH⊥AB，垂足是H，易得：EH= ，BH= ，FH= ．

在Rt△EHF中， ，∴（0＜x＜8）．

（2）取弧ED的中点P，联结BP交ED于点G．

∵ ，P是弧ED的中点，∴弧EP=弧EF=弧PD，∴∠FBE =∠EBP =∠PBD．

∵弧EP=弧EF ，BP过圆心，∴BG⊥ED，ED =2EG =2DG．

又∵∠CEA =∠DEB，∴∠CAE=∠EBP=∠ABC．

又∵BE是公共边，∴△BEH≌△BEG，∴EH=EG=GD= ．

在Rt△CEA中，∵AC = 6，BC=8，tan∠CAE=tan∠ABC=，∴CE=ACtan∠CAE==，∴BE==，∴ED=2EG= ==．

（3）四边形ABDC不可能为直角梯形．

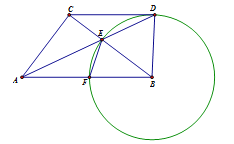
①当CD∥AB时，如果四边形ABDC是直角梯形，只可能∠ABD =∠CDB = 90o．

在Rt△CBD中，∵BC=8，∴CDcos∠BCD=，BD=BCsin∠BCD= =BE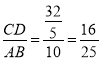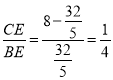，∴， ，∴，∴CD不平行于AB，与CD∥AB矛盾，∴四边形ABDC不可能为直角梯形．

②当AC∥BD时，如果四边形ABDC是直角梯形，只可能∠ACD =∠CDB = 90o．

∵AC∥BD，∠ACB = 90o，∴∠ACB =∠CBD = 90o，∴∠ABD =∠ACB +∠BCD ＞ 90o．

与∠ACD =∠CDB = 90o矛盾．

∴四边形ABDC不可能为直角梯形．