题目内容
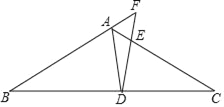
【题目】如图,在△ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DEDF.
(1)求证:△BFD∽△CAD;
(2)求证:BFDE=ABAD.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据相似三角形的判定得出△ADF∽△EDA,再利用相似三角形的性质得出∠F=∠DAE,进而证明△BFD∽△CAD即可;
(2)由(1)得出![]() ,再证明
,再证明![]() ,进而解答即可.
,进而解答即可.
试题解析:证明:(1)∵AD2=DEDF,∴![]() .∵∠ADF=∠EDA,∴△ADF∽△EDA,∴∠F=∠DAE.又∵∠ADB=∠CDE,∴∠ADB+∠ADF=∠CDE+∠ADF,即∠BDF=∠CDA,∴△BFD∽△CAD;
.∵∠ADF=∠EDA,∴△ADF∽△EDA,∴∠F=∠DAE.又∵∠ADB=∠CDE,∴∠ADB+∠ADF=∠CDE+∠ADF,即∠BDF=∠CDA,∴△BFD∽△CAD;
(2)∵△BFD∽△CAD,∴![]() ,∴
,∴![]() .∵△BFD∽△CAD,∴∠B=∠C,∴AB=AC,∴
.∵△BFD∽△CAD,∴∠B=∠C,∴AB=AC,∴![]() ,∴BFDE=ABAD.
,∴BFDE=ABAD.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 1 | 2 | 3 | 4 | … |
碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示).
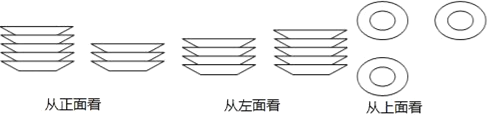
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
【题目】今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。”卖菜阿姨说:“下雪天从地里弄菜不容易啊,所以你花这些钱要比昨天少买1斤了。”王大爷回答道:“应该的,你们也真的辛苦。”
青菜 | 花菜 | 大白菜 | |
1月24日 | 2元/斤 | 5元/斤 | 1元/斤 |
1月25日 | 2.5元/斤 | 7元/斤 | 1.5元/斤 |
(1)请问超市三种蔬菜中哪种涨幅最大?并计算其涨幅;
(2)请你根据王大爷和卖菜阿姨的对话,来算算,这天王大爷买了几斤菠菜?