题目内容
【题目】某种蔬菜每千克售价
（元）与销售月份
之间的关系如图1所示，每千克成本
（元）与销售月份之间的关系如图2所示，其中图1中的点在同一条线段上，图2中的点在同一条抛物线上，且抛物线的最低点的坐标为（6，1）．
（1）求出与之间满足的函数表达式，并直接写出的取值范围；
（2）求出与之间满足的函数表达式；
（3）设这种蔬菜每千克收益为
元，试问在哪个月份出售这种蔬菜，
将取得最大值？并求出此最大值．（收益=售价-成本）
【答案】（1）y1=﹣
x+7（3≤x≤6）；（2）y2=
（x﹣6）2+1；（3）5月出售这种蔬菜，每千克收益最大
【解析】
（1）设y1=kx+b，y2=a（x-b）2+c，代入各点求出未知量，（2）收益=售价-成本，列出函数解析式，求出最大值．
（1）设y1=kx+b，
∵直线经过（3，5）、（6，3），
，解得：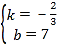
，
∴y1=﹣x+7（3≤x≤6），
（2）设y2=a（x﹣6）2+1，
把（3，4）代入得：4=a（3﹣6）2+1，
解得a=，
∴y2=（x﹣6）2+1，
（3）由题意得：w=y1﹣y2=﹣x+7﹣[（x﹣6）2+1]，
=﹣x2+
=﹣
，
当x=5时，y最大值=
．
故5月出售这种蔬菜，每千克收益最大．
【题目】王老师将
个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是________（精确到0.01）；
估算袋中白球的个数；
在的条件下，若小强同学有放回地连续两次摸球，用画树状图或列表的方法计算他两次都摸出白球的概率．
【题目】[问题情境]
已知矩形的面积为一定值1，当该矩形的一组邻边分别为多少时，它的周长最小？最小值是多少？
[数学模型]
设该矩形的一边长为x，周长为L，则L与x的函数表达式为 ．
[探索研究]
小彬借鉴以前研究函数的经验，先探索函数
的图象性质．
（1）结合问题情境，函数的自变量x的取值范围是 ，
如表是y与x的几组对应值．
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值；
②画出该函数图象，结合图象，得出当x= 时，y有最小值，y的最小值为 ．
[解决问题]
（2）直接写出“问题情境”中问题的结论．
