题目内容
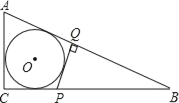
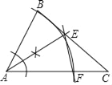
【题目】如图,在△ABC中,∠ABC=2∠C,依据尺规作图的痕迹,解答下面的问题:
(1)求证:△ABE≌△AFE;
(2)若AB=3.3,BE=1.8,求AC的长.
【答案】(1)见解析;(2)AC=5.1.
【解析】
(1)根据全等三角形的判定定理进行证明;
(2)利用(1)中全等三角形的对应边、对应角相等推知:∠C=∠FEC,结合等角对等边得到BC=FE,则FC=BE,结合图形求得答案.
(1)证明:由尺规作图的痕迹可知,AB=AF,
且AE是∠BAC的平分线,
∴∠BAE=∠FAE,
又AE=AE,
∴△ABE≌△AFE.
(2)由(1)中的结论可知,
AB=AF,BE=FE,∠ABE=∠AFE,
又∠ABC=2∠C,
∴∠AFE=2∠C,
∵∠AFE=∠C+∠FEC,
∴∠C=∠FEC,
∴FC=FE,
∴FC=BE,
故AC=AF+FC=AB+BE=3.3+1.8=5.1.

练习册系列答案
相关题目
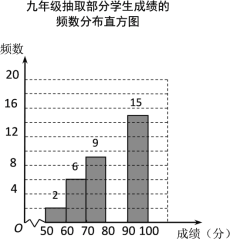
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
![]()
成绩x/分 | 频数 | 频率 | |
第1段 | x<60 | 2 | 0.04 |
第2段 | 60≤x<70 | 6 | 0.12 |
第3段 | 70≤x<80 | 9 | b |
第4段 | 80≤x<90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?