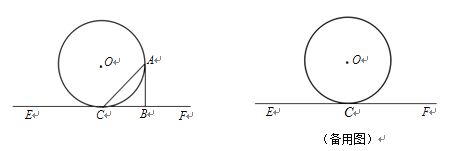Question

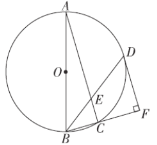
【题目】如图，AB是⊙O的直径，△ABC内接于⊙O．点D在⊙O 上，BD平分∠ABC交AC于点E，DF⊥BC交BC的延长线于点F．

（1）求证：FD是⊙O的切线；

（2）若BD=8，sin∠DBF=，求DE的长．

Answer 1

【答案】（1）详见解析；（2）

【解析】

(1)连接OD，根据角平分线的定义得到∠ABD=∠DBF，由等腰三角形的性质得到∠ABD=∠ODB，等量代换得到∠DBF=∠ODB，推出∠ODF=90°，根据切线的判定定理得到结论；

（2）连接AD，根据圆周角定理得到∠ADE=90°，根据角平分线的定义得到∠DBF=∠ABD，解直角三角形得到AD=6，在Rt△ADE中，解直角三角形得到DE=．

（1）连接OD，

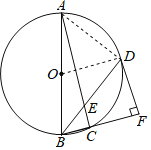
∵BD平分∠ABC交AC于点E，

∴∠ABD=∠DBF，

∵OB=OD，

∴∠ABD=∠ODB，

∴∠DBF=∠ODB，

∵∠DBF+∠BDF=90°，

∴∠ODB+∠BDF=90°，

∴∠ODF=90°，

∴FD是⊙O的切线；

（2）连接AD，

∵AB是⊙O的直径，

∴∠ADE=90°，

∵BD平分∠ABC交AC于点E，

∴∠DBF=∠ABD，

在Rt△ABD中，BD=8，

∵sin∠ABD=sin∠DBF=，

∴AB=10，AD=6，

∵∠DAC=∠DBC，

∴sin∠DAE=sin∠DBC=，

在Rt△ADE中，sin∠DAC=，

设DE=3x，则AE=5x，

∴AD=4x，

∴tan∠DAE=

∴DE=．