题目内容
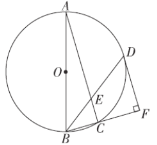
【题目】如图,直线EF与⊙O相切于点C,点A为⊙O上异于点C的一动点,⊙O的半径为4,AB![]() EF于点B,设
EF于点B,设![]() ACF=α(0°<α<180°).
ACF=α(0°<α<180°).
(1)若α=![]() ,求证:四边形OCBA为正方形;
,求证:四边形OCBA为正方形;
(2)若AC―AB=1,求AC的长;
(3)当AC―AB取最大值时,求α的度数.
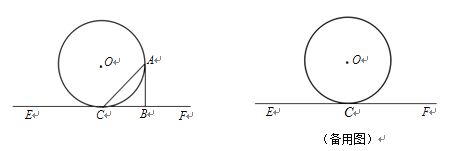
【答案】(1)见解析;(2)AC=![]() ;(3)∠α=
;(3)∠α=![]() 或
或![]()
【解析】
(1)连接OA,OC,证△ABC是等腰直角三角形,△OAC是等腰直角三角形,再证四边形OCBA为矩形
由OA=OC,得四边形OCBA为正方形;(2)作OH![]() AB,设AC=x,则AB=x-1,由勾股定理得,在Rt△OAH中,
AB,设AC=x,则AB=x-1,由勾股定理得,在Rt△OAH中,![]() ,在Rt△OEC中,
,在Rt△OEC中,![]() ,
,![]() ;(3)根据锐角三角函数和相似三角形性质可得出差的函数解析式,再求最值.
;(3)根据锐角三角函数和相似三角形性质可得出差的函数解析式,再求最值.
解:(1)连接OA,OC
∵α=![]() ,AB
,AB![]() EF
EF
∴△ABC是等腰直角三角形
∵EF与⊙O相切于C
∴∠OCB=![]()
∴∠OCA=![]()
∴△OAC是等腰直角三角形
∴∠OCB=∠CBA=∠COA=900
∴四边形OCBA为矩形
∵OA=OC
∴四边形OCBA为正方形
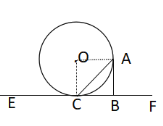
(2)如图,作OH⊥AB,
设AC=x,则AB=x-1

∵在Rt△OAH中,![]()
又∵在Rt△OEC中,![]()
∴![]()
∴![]()
即:AC=![]()
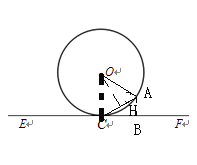
(3)如图,作OH⊥AC,则AC=2CH,设CH=x,AC=2x,
由(1)(2)可得
![]()
∴![]() ,即
,即![]()
∴AB=![]()
∴AC-AB=y=2x-![]() ,∵当x=2时,y最大.
,∵当x=2时,y最大.
此时,sinα=![]()
∴α=300
同理,当A在OC的左侧时,α=1500,AC-AB的值最大.
∴当AC-AB取最大值时,![]() α=
α=![]() 或
或![]()

【题目】合肥市教育教学研究室为了了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:![]() 等,130分
等,130分![]() 150分;
150分;![]() 等,110分
等,110分![]() 129分;C等,90分
129分;C等,90分![]() 109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 | 频数 | 频率 |
| 0.2 | |
| ||
| 6 | |
| 2 | 0.1 |
合计 | 1 |
2019年合肥市一模教学成绩频数分布直方图
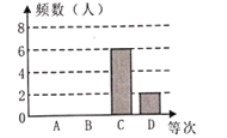
根据图表中的信息,下列说法不正确的是( )
A. 这次抽查了20名学生参加一模考试的数学成绩
B. 这次一模考试中,考试数学成绩为![]() 等次的频率为0.4
等次的频率为0.4
C. 根据频数分布直方图制作的扇形统计图中等次![]() 所占的圆心角为
所占的圆心角为![]()
D. 若全市有20000名学生参加中考一模考试,则估计数学成绩达到![]() 等次及以上的人数有12000人
等次及以上的人数有12000人