题目内容
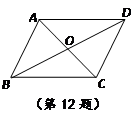
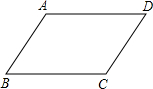
如图,四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构造命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)

(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)

(1)以①②作为条件构成的命题是真命题,
证明:∵AB∥CD,
 ∴∠OAB=∠OCD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
,
∴△AOB≌△COD,
∴OB=OD,
∴四边形ABCD是平行四边形.
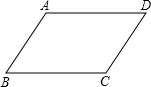
(2)根据①③作为条件构成的命题是假命题,即如果有一组对边平行,另一组对边相等,那么四边形是平行四边形,如等腰梯形符合,但不是平行四边形;
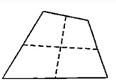
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形是平行四边形,如图,
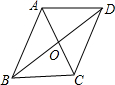
根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.
证明:∵AB∥CD,
 ∴∠OAB=∠OCD,
∴∠OAB=∠OCD,在△AOB和△COD中,
|
∴△AOB≌△COD,
∴OB=OD,
∴四边形ABCD是平行四边形.
(2)根据①③作为条件构成的命题是假命题,即如果有一组对边平行,另一组对边相等,那么四边形是平行四边形,如等腰梯形符合,但不是平行四边形;
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形是平行四边形,如图,

根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.

练习册系列答案
相关题目