题目内容
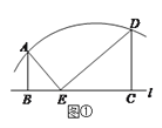
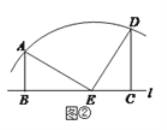
【题目】已知:如图,四边形ABCD为正方形, E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G。
(1)求证:DE+BG=EG;∠EAG=45°;
(2)AB=1,GF=m,FE=n,求m+n+mn的值;
(3)若AB=6,∠BAG=∠CEG,求GE.
【答案】
(1)
解:∵以AE为对称轴,作与△ADE成轴对称的图形△AFE,
∴△ADE≌△AFE,
∴AD=AF=AB,DE=FE,∠DAE=∠FAE,∠D=∠AFE=∠AFG=90°=∠B,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠EAG=∠FAE+∠FAG= ![]() ∠BAD=45°,
∠BAD=45°,
∴GE=GF+EF=BG+DE.
(2)
解:∵AB=1,GF=m,FE=n,则EG=m+n,CG=1-m,CE=1-n,
∵∠C=90°,
∴(1-m)2+(1-n)2=(m+n)2,
整理得:m+n+mn=1.
(3)
解:由(1)可得Rt△ABG≌Rt△AFG,
∴∠BGA=∠FGA.
∵∠BAG=∠CEG,
∴∠BGA=∠CGE,
∴∠BGA=∠CGE=∠FGA= ![]() .
.
则∠BAG=∠CEG=30°,
∴BG= ![]() AB=2
AB=2 ![]() ,
,
∴CG=AB-BG=6-2 ![]() ,
,
∴GE=2CG=12-4 ![]() .
.
【解析】(1)根据HL,Rt△ABG≌Rt△AFG,根据全等三角形的性质,及等量代换可解答;(2)在Rt△CEG中,由勾股定理可得CG2+CE2=EG2 , 将入相应的m,n的代数式,即可求得;(3)易证得到∠BGA=∠CGE=∠FGA= ![]() .则∠BAG=∠CEG=30°,再根据含30°角的直角三角形的三边关系,求出相应边的长度.
.则∠BAG=∠CEG=30°,再根据含30°角的直角三角形的三边关系,求出相应边的长度.

练习册系列答案
相关题目