Question

【题目】已知是一段圆弧上的两点，有在直线的同侧，分别过这两点作的垂线，垂足为， 是上一动点，连结，且．

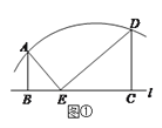
（1）如图①，如果，且，求的长．

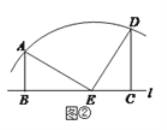
（2）（i）如图②，若点E恰为这段圆弧的圆心，则线段之间有怎样的等量关系？请写出你的结论并予以证明．

（ii）再探究：当分别在直线两侧且，而其余条件不变时，线段之间又有怎样的等量关系？请直接写出结论，不必证明．

Answer 1

【答案】（1）;（2）（i）,证明见解析;（ii）当A、D分别在直线两侧时，线段AB、BC、CD有如下等量关系： （）或（）.

【解析】解：（1）∵AB⊥于B，DC⊥于C，

∴∠ABE=∠ECD＝90°．

∵∠BEA+∠AED+∠CED=180°，且∠AED＝90°，

∴∠CED＝90°－∠BEA．

又∠BAE＝90°－∠BEA，

∴∠BAE＝∠CED．

∴Rt△ABE∽Rt△ECD．

（或：∵AB⊥于B，DC⊥于C，∴AB∥DC．∴Rt△ABE∽Rt△ECD）．

∴．

∵， ，

∴．

又，∴．

在中，由勾股定理，得

∴ ．

（2）（i）猜想： ．

证明：在Rt△ABE中，∵∠ABE=90°，

∴∠BAE=90°－∠AEB．

又∵∠AEB+∠AED+∠CED＝180°，

且∠AED＝90°，

∴∠CED=90°－∠AEB．

∴∠BAE＝∠CED．

∵DC⊥BC于点C，∴∠ECD＝90°．

由已知，有．

于是在Rt△ABE和Rt△ECD中，

∵∠ABE=∠ECD＝90°，∠BAE＝∠CED， ，

∴Rt△ABE≌Rt△ECD．（AAS）

∴．

∴．即．

（ii）当A、D分别在直线两侧时，线段AB、BC、CD有如下等量关系：

（）或（）.