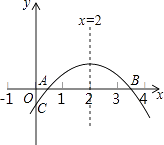题目内容
【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() (
(![]() )
)
【解析】
(1)先利用点A的坐标和勾股定理求出OA的长度,然后利用菱形的性质可求出点C的坐标,最后利用待定系数法即可求出直线AC的解析式;
(2)先利用菱形的性质证明![]() ,则有
,则有![]() 然后根据直线AC的解析式求出点D的坐标,最后利用三角形的面积公式
然后根据直线AC的解析式求出点D的坐标,最后利用三角形的面积公式![]() 求解即可.
求解即可.
(1)过点A作![]() 轴于点M,
轴于点M,

∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() .
.
∵四边形OABC是菱形,
∴![]() ,
,
∴![]() .
.
设直线AC的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线AC解析式为![]() ;
;
(2)如图,

∵四边形OABC是菱形,
∴![]() ,
,
![]() ,
,
![]() .
.
∵直线AC解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
【题目】某商店需要购进甲、乙两种商品共1000件,其进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 18 | 44 |
(1)若商店计划销售完这批商品后能获利4200元,则甲、乙两种商品应分别购进多少件;
(2)若该商店销售完这批商品后获利要多于5000元,则至少应购进乙种商品多少件?