Question

【题目】已知点M是等边△ABD中边AB上任意一点(不与A. B重合),作∠DMN=60，交∠DBA外角平分线于点N.

(1)求证：DM=MN；

(2)若点M在AB的延长线上，其余条件不变，结论“DM=MN”是否依然成立?请你画出图形并证明你的结论.

Answer 1

【答案】（1）见解析 （2）“DM=MN”依然成立，证明见解析

【解析】

（1）在AD上截取AF=AM，证明△DFM≌△MBN即可；
（2）在AD的延长线上截取AF=AM，证明△DFM≌△MBN即可．

（1）如图1，在AD上截取AF=AM，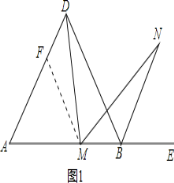

∵△ABD是等边三角形，

∴∠A=60°
∴△AMF是等边三角形，

∴∠AFM=60°
∴∠DFM=120°，

∵AB=AD，AM=AF

∴DF=MB，

∵∠ABD=60°

∴∠DBE=120°

∵BN是∠DBA外角平分线

∴∠DBN=60°
∴∠MBN=∠ABD +∠DBN =120°，
∴∠DFM=∠MBN，
∵∠DMN=60°，
∴∠BMN+∠AMD=120°，
∵∠A=60°，
∴∠FDM+∠AMD=120°，
∴∠FDM=∠BMN，
在△FDM和△BMN中，

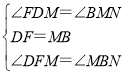
∴△FDM≌△BMN（ASA），
∴DM=MN．
（2）点M在AB的延长线上，如图2所示，在AD的延长线上截取AF=AM，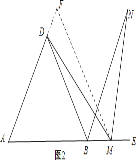

∵△ABD是等边三角形，

∴∠A=60°
∴△AMF是等边三角形，
∴∠DFM=60°，

∵AF=AM，AD=AB

∴DF=MB，

∵∠ABD=60°

∴∠DBE=120°

∵BN是∠DBA外角平分线

∴∠MBN=60°，
∴∠DFM=∠MBN，
∵∠BMN=∠AMD+∠DMN，∠FDM=∠A+∠AMD，
∠DMN=∠A=60°，
∴∠FDM=∠BMN，
在△FDM和△BMN中，

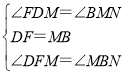
∴△FDM≌△BMN（ASA），
∴DM=MN．