题目内容
【题目】如图所示，三角形ABC的面积为4cm2．AP垂直∠B的平分线BP于点P．则三角形PBC的面积是__．
【答案】2cm2
【解析】
过点P作PE⊥BP，垂足为P，交BC于点E，由角平分线的定义可知∠ABP=∠EBP，结合BP=BP以及∠APB=∠EPB=90°即可证出△ABP≌△EBP（ASA），进而可得出AP=EP，根据三角形的面积即可得出S△APC=S△EPC，再根据S△PBC=S△BPE+S△EPC=
S△ABC即可得出结论．
延长AP,交BC于点E,如图所示。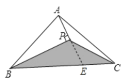
∵AP垂直∠B的平分线BP于点P，
∴∠ABP=∠EBP.
在△ABP和△EBP中,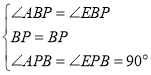 
，
∴△ABP≌△EBP(ASA)，
∴AP=EP.
∵△APC和△EPC等底同高，
S△PBC=S△BPE+S△EPC=S△ABC=2（cm2）.
故答案为2cm2.
练习册系列答案
相关题目
【题目】三台县某中学“五
四”青年节举行了“班班有歌声”歌咏比赛活动比赛聘请了10位教师和10位学生担任评委，其中甲班的得分情况如统计表和统计图．
老师评委评分统计表：
评委序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
分数 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
学生评委评分折线统计图师生评委评分频数分布直方图
补全频数分布直方图．
学生评委评分的中位数是______．
计分办法规定：老师评委、学生评委的评分各去掉一个最高分、一个最低分，并且按教师、学生各占
、
的方法计算各班最后得分，知甲班最后得分
分，试求统计表中的x．
