Question

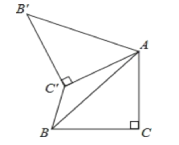
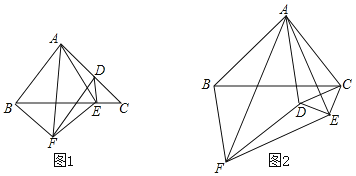
【题目】如图1，在△ABC中，∠BAC=90°，AB=AC，在△ABC内部作△CED，使∠CED=90°，E在BC上，D在AC上，分别以AB，AD为邻边作平行四边形ABFD，连接AF、AE、EF．

（1）证明：AE=EF；

（2）判断线段AF，AE的数量关系，并证明你的结论；

（3）在图（1）的基础上，将△CED绕点C逆时针旋转，请判断（2）问中的结论是否成立？若成立，结合图（2）写出证明过程；若不成立，请说明理由

Answer 1

【答案】（1）证明见解析；（2）AF=AE．证明见解析；（3）AF=AE成立．证明见解析.

【解析】

（1）根据△ABC是等腰直角三角形，△CDE是等腰直角三角形，四边形ABFD是平行四边形，判定△ACE≌△FDE（SAS），进而得出AE=EF；

（2）根据∠DFE+∠EAF+∠AFD=90°，即可得出△AEF是直角三角形，再根据AE=FE，得到△AEF是等腰直角三角形，进而得到AF=AE；

（3）延长FD交AC于K，先证明△EDF≌△ECA（SAS），再证明△AEF是等腰直角三角形即可得出结论．

（1）如图1，

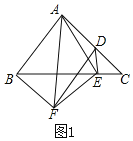
∵△ABC中，∠BAC=90°，AB=AC，

∴△ABC是等腰直角三角形，

∵∠CED=90°，E在BC上，D在AC上，

∴△CDE是等腰直角三角形，

∴CE=CD，

∵四边形ABFD是平行四边形，

∴DF=AB=AC，

∵平行四边形ABFD中，AB∥DF，

∴∠CDF=∠CAB=90°，

∵∠C=∠CDE=45°，

∴∠FDE=45°=∠C，

在△ACE和△FDE中，

，

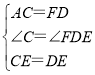∴△ACE≌△FDE（SAS），

∴AE=EF；

（2）AF=AE．

证明：如图1，∵AB∥DF，∠BAD=90°，

∴∠ADF=90°，

∴Rt△ADF中，∠DAE+∠EAF+∠AFD=90°，

∵△ACE≌△FDE，

∴∠DAE=∠DFE，

∴∠DFE+∠EAF+∠AFD=90°，

即△AEF是直角三角形，

又∵AE=FE，

∴△AEF是等腰直角三角形，

∴AF=AE；

（3）AF=AE仍成立．

证明：如图2，延长FD交AC于K．

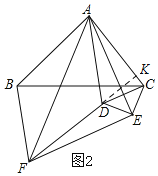
∵∠EDF=180°-∠KDC-∠EDC=135°-∠KDC，

∠ACE=（90°-∠KDC）+∠DCE=135°-∠KDC，

∴∠EDF=∠ACE，

∵DF=AB，AB=AC，

∴DF=AC，

在△EDF和△ECA中，

，

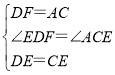∴△EDF≌△ECA（SAS），

∴EF=EA，∠FED=∠AEC，

∴∠FEA=∠DEC=90°，

∴△AEF是等腰直角三角形，

∴AF=AE．