题目内容
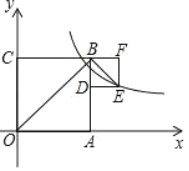
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
【答案】C
【解析】设E点坐标为(a,b),则AO+DE=a,AB﹣BD=b,根据△ABO和△BED都是等腰直角三
角形,得到EB=![]() BD,OB=
BD,OB=![]() AB,再根据OB2﹣EB2=10,运用平方差公式即可得到(AO+DE)(AB ﹣BD)=5,进而得到ab=5,据此可得k=5.
AB,再根据OB2﹣EB2=10,运用平方差公式即可得到(AO+DE)(AB ﹣BD)=5,进而得到ab=5,据此可得k=5.
设E点坐标为(a,b),则AO+DE=a,AB﹣BD=b,
∵△ABO和△BED都是等腰直角三角形,
∴EB=![]() BD,OB=
BD,OB=![]() AB,BD=DE,OA=AB,
AB,BD=DE,OA=AB,
∵OB2﹣EB2=10,
∴2AB2﹣2BD2=10,
即AB2﹣BD2=5,
∴(AB+BD)(AB﹣BD)=5,
∴(AO+DE)(AB﹣BD)=5,
∴ab=5,
∴k=5.
故选:C.

【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写下表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数_________________(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子____________个?
(4)计算前20个“T”字形图案中棋子的总个数.
(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?