题目内容
【题目】如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC= ![]() ,AD=
,AD= ![]() ,求DE的长.
,求DE的长. 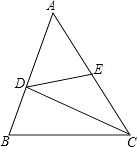
【答案】解:∵BD=1,DC=3,BC= ![]() ,
,
又∵12+32=( ![]() )2,
)2,
∴BD2+CD2=BC2,
∴△BCD是直角三角形且∠BDC=90°,
∴∠ADC=90°,
∴AC= ![]() =4,
=4,
又∵E点为AC的中点
∴DE= ![]() =2.
=2.
【解析】首先根据勾股定理的逆定理判定△BCD是直角三角形且∠BDC=90°,再利用勾股定理可求出AC的长,进而可求出DE的长.
【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.

练习册系列答案
相关题目