题目内容
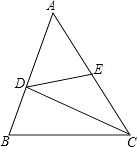
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
【答案】DE;BC;同位角相等,两直线平行;对顶角相等;DF;AB;同旁内角互补,两直线平行
【解析】试题分析:由同位角相等,两直线平行可得DE∥BC,由对顶角相等可得∠4=65°,再由同旁内角互补,两直线平行可得DF∥AB.
试题解析:因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以DE∥BC (同位角相等,两直线平行).
因为AB与DE相交,
所以∠1=∠4(对顶角相等).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以DF∥AB (同旁内角互补,两直线平行).

练习册系列答案
相关题目