题目内容
【题目】已知,O为直线AB上一点,∠DOE=90°.
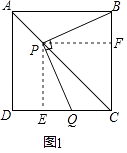
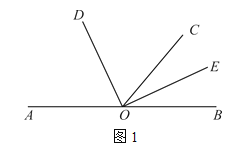
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
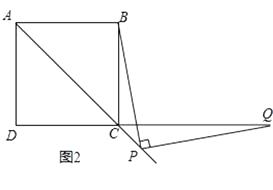
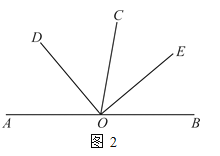
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
【答案】(1)①115°;②答案见解析;(2)∠AOD=50°
【解析】试题分析:(1)①先求出∠AOD的度数,再根据邻补角求出∠BOD即可;
②分别求出∠COE,∠BOE的度数即可作出判断;
(2)由已知设∠BOE=2x,则∠AOE=7x, 再根据∠BOE+∠AOE=180°,求出∠BOE=40°,再根据互余即可求出∠AOD=90°-40°=50°.
试题解析:(1)①∵OD平分∠AOC,∠AOC=130°,
∴∠AOD=∠DOC=![]() ∠AOC=
∠AOC=![]() ×130°=65°,
×130°=65°,
∴∠BOD=180°-∠AOD=180°-65°=115°;
②∵∠DOE=90°,又∠DOC=65°,
∴∠COE=∠DOE-∠DOC=90°-65°=25°,
∵∠BOD=115°,∠DOE=90°,
∴∠BOE=∠BOD-∠DOE=115°-90°=25°,
∴∠COE=∠BOE,
即OE平分∠BOC;
(2)若∠BOE:∠AOE=2:7,
设∠BOE=2x,则∠AOE=7x,
又∠BOE+∠AOE=180°,∴2x+7x=180°,
∴x=20°,∠BOE=2x=40°,
∵∠DOE=90°,
∴∠AOD=90°-40°=50°.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目