Question

【题目】如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，，，

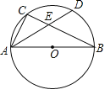
（1）连结OD，求证；

（2）求CD的长；

（3）求AE的长.

Answer 1

【答案】（1）证明见详解；

（2）6；
（3）.

【解析】

（1）连结OD，因为弦AD平分∠BAC，所以∠CAD=∠BAD，即，所以OD⊥CB；

（2）连结BD，则∠ADB=90°，因为AB=10，AD=8，所以BD=6，因为，所以CD=BD=6；

（3）证△CDE∽△ADC，可求得DE的长，进而得出AE的长．

解：（1）如图，连结OD，
∵弦AD平分∠BAC，
∴∠CAD=∠BAD，

∴

∴OD⊥CB；
（2）如图，连结BD，CD，
∵AB为⊙O的直径，
∴∠ADB=90°，
∵AB=10，AD=8，
∴，
∵，

∴CD=BD=6，
（3）∵∠DCB=∠DAB，∠CAD=∠DAB，
∴∠CAD=∠DCE，
∵∠CDE=∠ADC，
∴△CDE∽△ADC，
∴,即,

∴,

∴.