题目内容
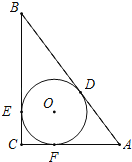
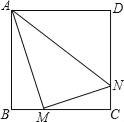
【题目】如图,矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长为__________.
的长为__________.
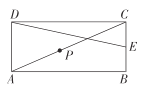
【答案】![]() 或
或![]()
【解析】
连结PD,PE,作EM⊥AC于M,DN⊥AC于N,分DE=PE,PE=PD,PD=DE三种情况讨论求解即可.
解:如图,连结PD,PE,作EM⊥AC于M,DN⊥AC于N,
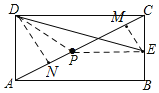
∵点E是BC的中点,
当DE=PE时,此时P于点A重合,
∵矩形ABCD的边AD=1,AB=2,
∴AC=![]() ,
,
∴CP的长为![]() ;
;
当PE=PD=x时,
在Rt△CME中,CM=CEcos∠ECM=![]() ,
,
EM=CEsin∠ECM=![]() ,
,
在Rt△PME中,PE2=EM2+PM2=(x![]() )2+(
)2+(![]() )2=x2
)2=x2![]() x+
x+![]() ,
,
同理,PD2=x2![]() x+4,
x+4,
∴x2![]() x+
x+![]() =x2
=x2![]() x+4,
x+4,
解得:x=![]() ,
,
当PD=DE时,不符合题意,舍去.
故答案为:![]() 或
或![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目