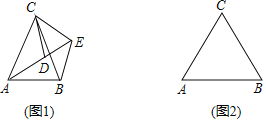Question

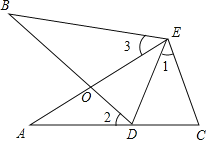
【题目】如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．

（1）求证：△AEC≌△BED；

（2）若∠1＝50°，则∠BDE＝　 　°．

Answer 1

【答案】（1）详见解析；（2）65．

【解析】

（1）要证明△AEC≌△BED，只要求得∠AEC＝∠BED即可，根据∠1＝∠2和三角形内角和可以得到∠AEC＝∠BED，然后写出△AEC≌△BED的条件，即可证明结论成立；

（2）根据（1）中证明的结论和等腰三角形的性质，可以求得∠ECD的度数，然后即可求得∠BDE的度数．

（1）证明：∵∠B＝∠A，∠BOE＝∠AOD，

∴∠3＝∠2，

∵∠1＝∠2，

∴∠3＝∠1，

∴∠3+∠AED＝∠1+∠AED，

∴∠BED＝∠AEC，

在△AEC和△BED中

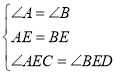
∴△AEC≌△BED（ASA）；

（2）∵△AEC≌△BED，

∴EC＝ED，

∴∠EDC＝∠ECD，

∵∠1＝50°，∠1＝∠2，

∴∠EDC＝∠ECD＝（180°－∠1）=65°，∠2＝50°，

∴∠BDE＝180°﹣∠2﹣∠EDC＝65°，

故答案为：65．