题目内容
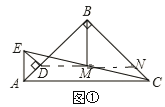
【题目】已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
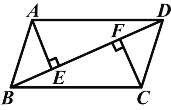
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为______________;
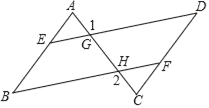
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.

【答案】BD=![]() BM
BM
【解析】(1)根据等腰直角三角形的性质,根据“直角三角形斜边上的中线等于斜边的一半”可知BD=![]() BM;
BM;
(2)先证明△MDE≌△MFC,得出AD=ED=FC,再作AN⊥EC于点N,证出△DBF是等腰直角三角形,根据点M是DF的中点,得出△BMD是等腰直角三角形,即可得出BD=![]() BM.
BM.
(1)∵∠ABC=∠ADE=90°,
∴ED∥BC,
∴∠DEM=∠MCB,
在△EMD和△CMN中
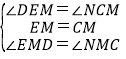
∴△EMD≌△CMN(ASA),
∴CN=DE=DA,MN=MD,
∵BA=BC,
∴BD=BN,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,∠DBM=![]() ∠DBN=45°=∠BDM,
∠DBN=45°=∠BDM,
∴△BMD为等腰直角三角形.
∴BD=![]() BM,
BM,
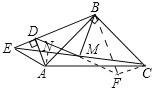
(2)结论成立.
证明:过点C作CF∥ED,与DM的延长线交于点F,连接BF,
可证得△MDE≌△MFC,
∴DM=FM,DE=FC,
∴AD=ED=FC,
作AN⊥EC于点N,
由已知∠ADE=90°,∠ABC=90°,
可证得∠DEN=∠DAN,∠NAB=∠BCM,
∵CF∥ED,
∴∠DEN=∠FCM,
∴∠BCF=∠BCM+∠FCM=∠NAB+∠DEN=∠NAB+∠DAN=∠BAD,
∴△BCF≌△BAD,
∴BF=BD,∠DBA=∠CBF,
∴∠DBF=∠DBA+∠ABF=∠CBF+∠ABF=∠ABC=90°,
∴△DBF是等腰直角三角形,
∵点M是DF的中点,
则△BMD是等腰直角三角形,
∴BD=![]() BM.
BM.

 阅读快车系列答案
阅读快车系列答案