题目内容
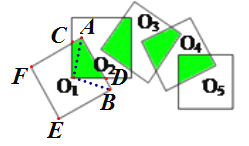
【题目】将5个边长为1的正方形按照如图所示方式摆放,O1,O2,O3,O4,O5是正方形对角线的交点,那么阴影部分面积之和等于________.

【答案】1 .
【解析】连接O1A,O1B,先证明△AO1C≌△BO1D,从而可得S四边形ACO1D=S△AO1B=![]() S正方形ABEF=
S正方形ABEF=![]() ,然后可求阴影部分面积之和.
,然后可求阴影部分面积之和.
如图,连接O1A,O1B.
∵四边形ABEF是正方形,
∴O1A=O1B, ∠AO1B=90°.
∵∠AO1C+∠AO1D=90°, ∠BO1D+∠AO1D=90°,
∴∠AO1C=∠BO1D.
在△AO1C和△BO1D中,
∵∠AO1C=∠BO1D,
O1A=O1B,
∠O1AC=∠O1BD=45°,
∴△AO1C≌△BO1D,
∴S四边形ACO1D=S△AO1B=![]() S正方形ABEF=
S正方形ABEF=![]() ,
,
∴阴影部分面积之和等于![]() ×4=1.
×4=1.
故答案为:1.

练习册系列答案
相关题目