题目内容
【题目】已知：抛物线y=ax2+bx﹣3经过点A（7，﹣3），与x轴正半轴交于点B（m，0）、C（6m、0）两点，与y轴交于点D．
（1）求m的值；
（2）求这条抛物线的表达式；
（3）点P在抛物线上，点Q在x轴上，当∠PQD=90°且PQ=2DQ时，求点P、Q的坐标．
【答案】
（1）
解：当x=0时，y=﹣3，
∴D（0，﹣3）．
设抛物线的解析式为y=a（x﹣m）（x﹣6m）．
把点D和点A的坐标代入得：6am2=﹣3①，a（7﹣m）（7﹣6m）=﹣3②，
∴a（7﹣m）（7﹣6m）=6am2．
∵a≠0，
∴（7﹣m）（7﹣6m）=m2．
解得：m=1
（2）
解：∵6am2=﹣3，
∴a=﹣ 
=﹣ 
．
将a=﹣ ，m=1代入得：y=﹣ x2+ 
x﹣3．
∴抛物线的表达式为y=﹣ x2+ x﹣3
（3）
解：如图所示：过点P作PE⊥x轴，垂足为E．
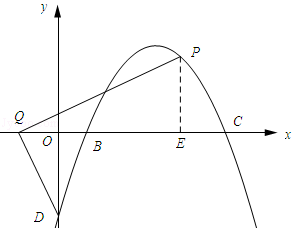
设点Q的坐标为（a，0）则OQ=﹣a
﹣∵∠DQP=90°，
∴∠PQO+∠OQD=90°．
又∵∠ODQ+∠DQO=90°，
∴∠PQE=∠ODQ．
又∵∠PEQ=∠DOQ=90°，
∴△ODQ∽△EQP．
∴ 
= 
= 
= ，即 
= 
= ，
∴QE=6，PE=﹣2a．
∴P的坐标为（a+6，﹣2a）
将点P的坐标代入抛物线的解析式得：﹣ （a+6）2+ （a+6）﹣3=﹣2a，整理得：a2+a=0，
解得a=﹣1或a=0．
当a=﹣1时，Q（﹣1，0），P（5，2）；当a=0时，Q（0，0），P（6，0）．
综上所述，Q（﹣1，0），P（5，2）或者Q（0，0），P（6，0）
【解析】（1）先求得点D的坐标，然后设抛物线的解析式为y=a（x﹣m）（x﹣6m），把点D和点A的坐标代入可求得m的值；（2）由6am2=﹣3，m=1可求得a的值，然后代入抛物线的解析式即可；（3）过点P作PE⊥x轴，垂足为E．设点Q的坐标为（a，0）则OQ=﹣a，然后证明△ODQ∽△EQP，依据相似三角形的性质可求得QE=6，PE=﹣2a，则P的坐标为（a+6，﹣2a），将点P的坐标代入抛物线的解析式可求得a的值．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
