题目内容
【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据: ![]() =1.4,
=1.4, ![]() =1.7,
=1.7, ![]() =2.4).
=2.4).
【答案】
(1)
解:延长BA交EF于点G,在Rt△AGE中,
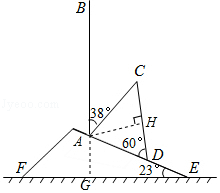
∵∠E=23°,
∴∠GAE=67°.
又∵∠BAC=38°,
∴∠CAE=180°﹣67°﹣38°=75°
(2)
解:过点A作AH⊥CD,垂足为H.
在△ADH中,
∵∠ADC=60°,AD=6m,
∴DH=ADcos∠ADC=6cos60°=3,AH=ADsin∠ADC=6sin60°=3 ![]() .
.
在Rt△ACH中,∠C=180°﹣75°﹣60°=45°,
∴CH=AH=3 ![]() ,
,
∴AC= ![]() =
= ![]() =
= ![]() =3
=3 ![]()
∴AB=AC+CD=3 ![]() +3
+3 ![]() +3≈15(米)
+3≈15(米)

【解析】(1)延长BA交EF于点G,根据直角三角形的性质求出∠GAE的度数,再由补角的定义即可得出结论;(2)过点A作AH⊥CD,垂足为H,在△ADH中,利用锐角三角函数的定义求出DH的长,同理可得出AC的长,由AB=AC+CD即可得出结论.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).

练习册系列答案
相关题目