题目内容
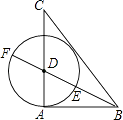
【题目】矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF,∠ECA=∠FCA.
(1)求证:四边形AFCE是菱形;
(2)若AB=8,BC=4,求菱形AFCE的面积.

【答案】(1)证明见解析;(2)20.
【解析】分析:(1)先证明四边形AFCE是平行四边形,再证明FA=FC,根据有一组邻边相等的平行四边形是菱形得出结论;
(2)设DE=x,则AE=EC=8-x,在Rt△ADE中,由勾股定理列方程求得x的值,再求菱形的面积即可.
详解:(1)∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∵DE=BF,
∴EC=AF,
而EC∥AF,
∴四边形AFCE是平行四边形,
由DC∥AB可得∠ECA=∠FAC,
∵∠ECA=∠FCA,
∴∠FAC=∠FCA,
∴FA=FC,
∴平行四边形AFCE是菱形;
(2)解:设DE=x,则AE=EC=8-x,
在Rt△ADE中,由勾股定理得
42+x2=(8-x)2,
解得x=3,
∴菱形的边长EC=8-3=5,
∴菱形AFCE的面积为:4×5=20.

练习册系列答案
相关题目
【题目】![]() 市、
市、![]() 市和
市和![]() 市分别有某种机器
市分别有某种机器![]() 台、
台、![]() 台、
台、![]() 台,现在决定把这些机器支援给
台,现在决定把这些机器支援给![]() 市
市![]() 台,
台,![]() 市
市![]() 台.己知调运机器的费用如表所示.
台.己知调运机器的费用如表所示.
|
|
| |
|
|
|
|
|
|
|
|
设从![]() 市、
市、![]() 市各调
市各调![]() 台到
台到![]() 市.
市.
(1)![]() 市调运到
市调运到![]() 市的机器为________台 (用含
市的机器为________台 (用含![]() 的式子表示);
的式子表示);
(2)![]() 市调运到
市调运到![]() 市的机器的费用为________元(用含
市的机器的费用为________元(用含![]() 的式子表示,并化简);
的式子表示,并化简);
(3)求调运完毕后的总运费(用![]() 的式子表示,并化简);
的式子表示,并化简);
(4)当![]() 和
和![]() 时,哪种调运方式总运费少?少多少?
时,哪种调运方式总运费少?少多少?