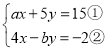题目内容
【题目】若抛物线
（t为实数）在
的范围内与x轴有公共点， 则t的取值范围为（ ）
A. 0＜t＜4 B. 0≤t＜4 C. 0＜t＜1 D. t≥0
【答案】B
【解析】先利用配方法得到抛物线的顶点为（2，-t），再分类讨论：当抛物线与x轴的公共点为顶点时，-t=0，解得t=0；当抛物线在0＜x＜3的范围内与x轴有公共点，如图，顶点在x轴下方，所以t＞0，当抛物线在原点与对称轴之间与x轴有交点时，x=0，y＞0，所以4-t＞0，解得t＜4；当抛物线在（3，0）与对称轴之间与x轴有交点时x=3，y＞0，即1-t＞0，解得t＜1，所以此时t的范围为0＜t＜4，综上两种情况即可得到t的范围为0≤t＜4．
y=x2-4x+4-t=（x-2）2-t，
抛物线的顶点为（2，-t），
当抛物线与x轴的公共点为顶点时，-t=0，解得t=0，
当抛物线在0＜x＜3的范围内与x轴有公共点，如图，
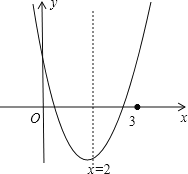
-t＜0，解得t＞0，则x=0时，y＞0，即4-t＞0，解得t＜4；x=3时，y＞0，即1-t＞0，解得t＜1，此时t的范围为0＜t＜4，
综上所述，t的范围为0≤t＜4．
故选B．
练习册系列答案
相关题目
