题目内容
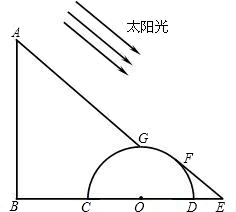
街道旁边有一根电线杆AB和一块半圆形广告牌,有一天,小明突然发现,在太阳光照射下,电线杆的顶端A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E,已知BC=5米,半圆形的直径为6米,DE=2米.
(1)求电线杆落在广告牌上的影长(即弧CG的长度,精确到0.1米);
(2)求电线杆的高度.
(1)求电线杆落在广告牌上的影长(即弧CG的长度,精确到0.1米);
(2)求电线杆的高度.

(1)∵G是半圆形广告牌的最高处,
∴
=
∵
为半圆,半圆直径为6米,
∴
=
dπ=
×6π=3π,
∴
=
≈4.7(米),
∴电线杆落在广告牌上的影长约为4.7米.
(2)连接OF,过点G作GH⊥AB于H,则BOGH是矩形.
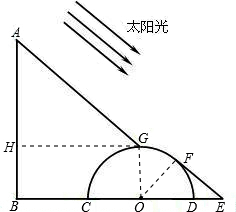
OG=3,BO=BC+CO=8,
∴BH=3,GH=8.
∵FE是⊙O的切线,
∴∠OFE=90°
∴FE=
=4.
∵太阳光线是平行光线,
∴AG∥EF,
又∵GH∥OE,
∴∠E=∠AGH.
又∵∠OFE=∠AHG=90°,
∴△AGH∽△OEF,
∴
=
,即
=
,
解得AH=6.
即AB=AH+HB=6+3=9.
答:电线杆落在广告牌上的影长约为4.7米,电线杆的高度为9米.
∴
 |
| CG |
| 1 |
| 2 |
 |
| CD |
∵
 |
| CD |
∴
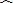 |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |
∴
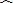 |
| CG |
| 3π |
| 2 |
∴电线杆落在广告牌上的影长约为4.7米.
(2)连接OF,过点G作GH⊥AB于H,则BOGH是矩形.

OG=3,BO=BC+CO=8,
∴BH=3,GH=8.
∵FE是⊙O的切线,
∴∠OFE=90°
∴FE=
| OE2-OF2 |
∵太阳光线是平行光线,
∴AG∥EF,
又∵GH∥OE,
∴∠E=∠AGH.
又∵∠OFE=∠AHG=90°,
∴△AGH∽△OEF,
∴
| FE |
| HG |
| OF |
| AH |
| 4 |
| 8 |
| 3 |
| AH |
解得AH=6.
即AB=AH+HB=6+3=9.
答:电线杆落在广告牌上的影长约为4.7米,电线杆的高度为9米.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目