题目内容
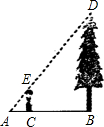
为测量被荷花池相隔的两树A、B的距离，数学活动小组设计了如图所示的测量方案：在AB的垂线AP上取两点C、E，再定出AP的垂线FE，使F、C、B在一条直线上．其中三位同学分别测量出了三组数据：
（1）AC、∠ACB；
（2）AC、CE；
（3）EF、CE、AC．
能根据所测数据，求得A、B两树距离的是（ ）
（1）AC、∠ACB；
（2）AC、CE；
（3）EF、CE、AC．
能根据所测数据，求得A、B两树距离的是（ ）
| A．（1） | B．（1），（2） | C．（2），（3） | D．（1），（3） |
∵AB⊥AP，EF⊥AP
∴AB∥EF
（1）tan∠ACB=
∴AB=AC•tan∠ACB
（3）EF：AB=CE：CA
∴AB=
∴能求出A、B两树距离的条件是（1）（3）
故选D．
∴AB∥EF
（1）tan∠ACB=
| AB |
| AC |
∴AB=AC•tan∠ACB
（3）EF：AB=CE：CA
∴AB=
| EF•AC |
| CE |
∴能求出A、B两树距离的条件是（1）（3）
故选D．
练习册系列答案
相关题目
