题目内容
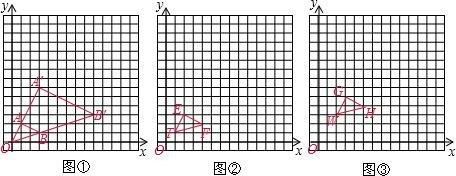
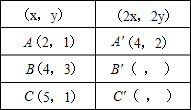
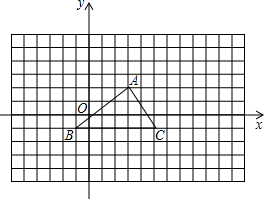
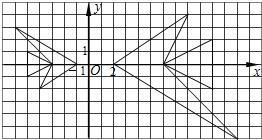
如图，△ABC与△A′B′C′是位似图形，且顶点都在格点上，则△ABC与△A′B′C′的相似比为______．面积比是______，位似中心的坐标是______．
连接B′B、A′A相交于点O′，即点O′为其位似中心．
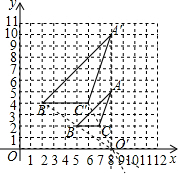
由图中BC边与B′C′的长可得其对应边的长的比为1：2，所以其位似比为1：2，其面积比为1：4，
由于点O′为其位似中心，
∴O′A=AA′，AA′=5，
∴点O′的纵坐标为0，
由于点C与点C′的横坐标相距1个单位长度，点C的横坐标为7，所以其位似中心的横坐标为8，
故其位似中心的坐标为（8，0）．
故答案为：1：2，1：4，（8，0）．
由图中BC边与B′C′的长可得其对应边的长的比为1：2，所以其位似比为1：2，其面积比为1：4，
由于点O′为其位似中心，
∴O′A=AA′，AA′=5，
∴点O′的纵坐标为0，
由于点C与点C′的横坐标相距1个单位长度，点C的横坐标为7，所以其位似中心的横坐标为8，
故其位似中心的坐标为（8，0）．
故答案为：1：2，1：4，（8，0）．
练习册系列答案
相关题目
所示）．则小鱼上的点（a，b）对应大鱼上的点（ ）
